[出处] 教育教学论坛_2021年第47期

宋娟

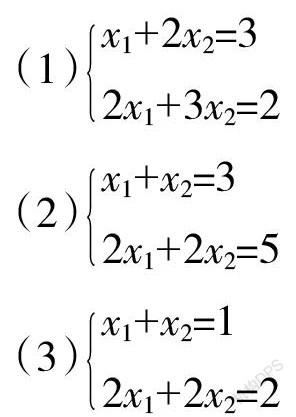
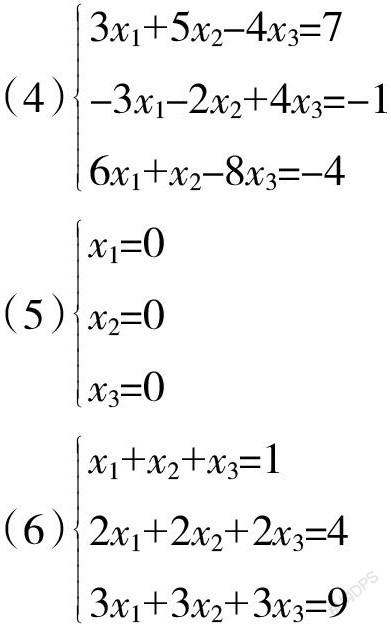
[关键词] 线性代数; 线性方程组;形象化教学;应用举例;考核方式

[基金项目] 2019年度江南大学教改项目“全英文大学数学课程研究与建设”（JG2019096）

[作者简介] 宋 娟（1982—），女，江苏宿迁人，博士，江南大学理学院讲师，主要从事计算数学研究。

[中图分类号] G642? ?[文献标识码] A? ?[文章编号] 1674-9324（2021）47-0091-04? ? [收稿日期] 2021-05-06

一、引言

“线性代数”是大学阶段理工科、经济、管理等专业必修的一门重要的数学基础课程，对学生数学思维能力的培养、后期专业课程的学习、编程能力的培养、解决问题及创新实践能力的培养具有重要的作用[1，2]。但是，据调研，学生对“线性代数”的学习往往停留在记概念、记定理，甚至做题思路都是死记硬背的层面，对其中的概念等理论知识往往不能真正理解，从而不能真正体会“线性代数”的意义。因此，课程学完后往往不能应用线性代数去解决实际问题。

事实上，“线性代数”中很多概念具有深远的意义，且“线性代数”在诸多领域如计算机图形学、预测及优化中均有广泛的应用。那么，如何把抽象的线性代数，以形象、易懂的方式呈现给学生，并用有趣的例子展示线性代数的广泛应用，激发学生学习线性代数的主观能动性，是我们应该深刻思考的问题。

下面结合笔者的教学经验，举例阐述线性代数概念的形象化教学，基于线性代数的应用举例来激发学生学习线性代数的内在动力。通过线性代数的国内国际教材对比分析，及国内的教学环境分析，认为通过适当调整“线性代数”的考核方式可以有效适应线性代数的现代化教学需求。

二、线性方程组解的概念的形象化教学

线性方程组的解是线性代数的主线，也是线性代数的重点和难点内容，在科学、工程和生活中均具有广泛的应用。针对此，本文以线性方程组的解为例，从几何的角度对这个概念进行形象化阐述，帮助学生更好地掌握这个概念，为学生以后利用这个知识点解决问题奠定一定的基础。

线性方程组的解，从几何图形上看，可以看成线性方程组中各个方程所对应的图形的交集。下面，分别以包含两和三个未知变量的线性方程组为例进行说明，含有多个未知变量的多元线性方程组可以在此基础上进行自然的推广。下面首先以三个二元线性方程组为例进行说明。

二元一次方程表示一条直线。很显然，方程组（1）中两个方程所对应的直线的斜率不同，所以是两条相交的直线，两相交直线的交集为其交点，此时，交点为方程组的唯一解;方程组（2）中两个方程对应的直线的斜率相同，但截距不同，所以是两条平行的直线，兩平行直线无交集，此时，方程组无解;方程组（3）中两个方程对应的直线的斜率相同，截距相同，是两条重合的直线，两重合直线的交集为这条直线上所有点，此时，方程组有无穷多解，即为直线上所有的点。

把上面的几何语言引入矩阵的秩进行重新阐述，即为线性方程组解的判定定理。再以三元线性方程组为例进行说明。

由空间解析几何知，对于方程组（4），第一个方程表示法向量为n1=（3，5，-4）的平面，第二个方程表示法向量为n2=（-3，-2，4）的平面，第三个方程表示法向量为n3=（6，1，-8）的平面，三个平面的法向量既不平行，也不垂直，是三个两两相交且不垂直的平面。因第一个平面和第二个平面的交线L的方向向量为n1×n2=（12，0，9），第二个平面和第三个平面交线M的方向向量为n2×n3=（12，0，9），第一个平面和第三个平面交线K的方向向量为n1×n3=（12，0，9），很显然，直线L、M与K的方向向量相同，且直线L、M和K均过点（1/3，2，1），因此三个平面的交集为直线L，直线L上所有点为第一个方程组的解。此时，方程组有无穷多解。

对于方程组（5），三个方程表示三维空间直角坐标系中相互垂直的三个平面，原点为唯一交点，此时，原点为方程组唯一解。

对于方程组（6），三个平面的法向量互相平行，且第一个方程过（0，0，1）点，不在第二个方程和第三个方程确定的平面上，第二个方程过（0，0，2）点，不在第一个方程和第三个方程确定的平面上，第三个方程过（0，0，3）点，不在第一个方程和第二个方程确定的平面上。因此，三个方程所确定的三个平面是互相平行且不重合的，此时，方程组无解。

类似地，对于包含三个未知数的方程组的解，在引入矩阵的秩后，可以将上面的几何语言采用系数矩阵的秩和增广矩阵的秩的关系重新阐述为线性方程组解的判定定理。

三、“线性代数”应用举例

为了进一步激发学生学习“线性代数”的兴趣，让学生感受线性代数是因用而学，且学习的目的是学以致用，下面以“线性代数”在计算机图形学以及未来预测中的应用为例进行阐述。

（一）计算机图形学中的应用：物体的投影

三维物体在二维计算机屏幕上的显示方法就是把它投影到一个可视平面上。三维物体和二维物体若仅考虑其形状，则物体上每一点有其对应的坐标（x，y，z），那么它投影到计算机屏幕上的坐标（x*，y*，0）是如何确定的？这个问题可以利用线性代数中的线性变换来实现。

例：设三维空间中一长方体的8个顶点坐标分别为（4，1，6），（5，1，6），（5，0，6），（4，0，6），（4，1，2），（5，1，2），（5，0，2），（4，0，2），求此长方体在投影中心为（0，0，9）的透视投影下的像。

投影坐标可用投影矩阵P及长方体三维坐标对应的齐次坐标构成的矩阵得到。

每一列的前三行除以第四行的对应元素所对应的点即为长方体投影后计算机屏幕上图形的顶点。上面的这个例子显示，基于“线性代数”中矩阵的乘法，可以方便确定出空间三维物体在计算机屏幕上的显示图形。

（二）未来预测中的应用

因未来预测在生活、商业中具有重要作用，下面我们以线性代数在未来预测中的应用为例。假设A市只有一个机场、市中心和火车站。在A市，出租车公司大约有3000辆汽车，开始分配在机场、市中心和火车站三个点的车辆分别为500、1500、1000。据统计，出租车由机场出租后回到机场、市中心、火车站的概率分别为0.9、0.01、0.09，由市中心出租后回到机场、市中心、火车站的概率分别为0.01、0.9、0.09，由火车站出租后回到机场、市中心、火车站的概率分别为0.09、0.01、0.9。那么，第六天机场、市中心、火车站三个站点分别有多少辆出租车被租出或准备出租？随着天数的增加，三个地点所需的出租車辆会不会大约固定，若固定，三个站点该如何分配出租车的比例？

显然，第五天各个站点的车辆分别768、958、1274辆。

即三个站点分配的出租车基本固定，大约为210、450、2340辆。

四、结语

本文以线性方程组的解为例，对“线性代数”中的抽象概念进行其几何意义下的阐述讲解，从而将抽象的线性代数概念形象化，帮助学生进一步理解概念、升华概念，为提高学生的数学素养奠定一定的基础。为进一步提高学生的学习兴趣，促进学生认识到“线性代数”是以需求为牵引，内需为导向，介绍了“线性代数”中的线性变换在计算机图形学中及在未来预测中的应用，激发了学生学习线性代数的内驱力，进一步培养了学生利用线性代数知识解决问题的能力。

最后，基于中外线性代数教材的比较[1，3]及国内的教学环境分析，笔者认为多元化“线性代数”的考核方式可以有效促进线性代数的教学与国际接轨，适应现代化教学需求。

目前，国内高校“线性代数”考核方式基本是闭卷考试，能较好考查学生掌握教材上基本知识点的情况，也能有效促进学生在较短时间内掌握用途较多的“线性代数”这门课的基本知识点。但是，目前国内的教材关于一些概念的背景及应用与国外的教材相比，还是相对较少的。

为了弥补这方面的不足，可以考虑将“线性代数”的考核按比例分为闭卷和开卷两部分。闭卷部分就是我们目前的考试方式，占考核的主要比例。开卷部分可以设为类似于国外线性代数教材中的应用性问题的考核，考查学生运用所学知识解决实际问题的能力，以考促学，考学相长，提高学生解决问题的能力及学生综合数学素养，以适应现代化的线性代数教学需求。